NSC-Math-181

Contact Information

Instructor: Serge Ballif
Email: Please use the Piazza discussion board in the left panel of Canvas.
Telephone: (702) 992-2613
Office Hours: NSE 114 Mon/Wed/Fri 9:00-9:20, 12:30-1:30, Tue/Thu 10:00-11:00. Drop by my office any time for help.

Course Learning Outcomes

A successful Math 181 student will demonstrate evidence of mastery of each of the following learning outcomes:

1. Calculate and Interpret Average Rates of Change
   
   • Numerically calculate an average rate of change from context.
   • Use correct units.
   • Explain the meaning of an average rate of change in context.
   • Describe the visual representation of average rates of change.
2. Approximating Instantaneous Rates of Change
   • Accurately describe average rates of change as approximations for the derivative (instantaneous rate of change).
   • Determine and explain when average rates of change are under or overestimates.
   • Demonstrate
3. Linearization and Approximations
   • Use the derivative to approximate values of a function.
   • Recognize when a function is not locally linear and include a prcise explanation of why.
4. Interpretation of the Derivative
   • Describe the units of the derivative.
   • Explain the meaning of values of the derivative in context (with complete sentences).
   • Interpret the value of the derivative as the slope of the tangent line at a point.
5. Relationships between a function and its derivative.
   • Given a function, be able to sketch the derivative function.
   • Explain the relationships between functions and their derivative (using words like increasing, decreasing, positive, negative, concave up, and conecave down) using tables of data, graphs, or functinos.
   • Use the derivative to find local minimum and maximum values and interpret these points in context.
6. Basic Derivative Rules
   • Calculate the derivatives of polynomials, exponential functions, logarithmic functions, and trigonometric functions.
7. Product and Quotient Rule
   • Calculate the derivative of products or quotients of functions
   • Symbolically apply the product and quotient rules when explicit functions are not given.
8. Chain Rule
   • Calculate the derivatives of compositions of functions
   • Find and interpret derivatives of implicit functions.
9. Intervals of Increase and Decrease
   • Identify intervals where a function is increasing or decreasing.
   • Use a calculus-based test to find minimum and maximum values of a function.
10. Concavity and Inflection Points
    • Identify intervals where a function is concave up or concave down.
    • Find and interpret inflection points in the context of a problem.
    • Use a calculus-based test to justify conclusions
11. Related Rates
    • Describe the relationship between the rate of change of a composition of functions and the rates of change of the composed functions.
    • Find the rate of change of a quantity by knowing the rate of change of a related quantity.
    • Accurately summarize a solution to a related rates problem with a sentence that includes units.
12. Optimization
    • Use the derivative to find minimum and maximum values of a function in context.
    • Find reasonable domains for functinos in context, and find the maxima and minima on these restricted domains.
    • Accurately summarize and interpret a solution to an optimization problem with a sentence (including units).
13. Compute and Interpret Riemann Sums
    • Use Riemann Sums to approximate accumulations in context.
    • Use correct units.
    • Explain the meaning of a Riemann sum calculation in context and any simplifying assumptions made to construct the sum.
14. Meaning of the Definite Integral
    • Construct and expression for the definite integral.
    • Explain the meaning of a definite integral in context.
    • Interpret a definite integral as an area.
15. Evaluate Definite Integrals.
    • Calculate the antiderivative of a function using the reverse of basic derivative rules.
    • Calculate the value of a definite integral using the Fundamental Theorem of Calculus.
16. Antiderivatives
    • Find antiderivatives of power functions, exponential functions, and trigonometric functions.
    • Use $u$-substitution to evaluate integrals.

Quick Grade Summary

Except for the WeBWorK HW, all of the work in the course will be graded on a PASS/NO PASS basis. The Schedule tells when outside work is due and the Specifications give the details on how to get a checkmark.

The rest of the syllabus explains more details about what these categories are.

Course Materials

Textbook: Active Calculus by Matt Boelkins et al. This is a free PDF download at http://gvsu.edu/s/xr or webpage at http://faculty.gvsu.edu/boelkinm/Home/AC/index.html. If you would like a print copy, see the link at the bottom of that page. We will be working through Sections 1.1–5.3 of this textbook. Video materials: All course pre-lectures are on a YouTube playlist at http://bit.ly/GVSUCalculus. Software: The course uses three software tools:

• Canvas is the course management system where our course home page is hosted.
• Desmos , a free program for graphing functions and building models. Guided Practice assignments will be completed using Desmos.
• WeBWorK is our online homework system. WeBWorK can be accessed using the link in the left-hand menu of our Canvas course.

Assigned Work

The work you do in the course has two purposes: To help you make sense of the concepts you are supposed to know, and to assess how well you have mastered the learning objectives of the course. These items of work include:

• Guided Practice: These are structured activities that guide you (by questions that you answer) through reading, viewing, and other preparatory activities on new content.
• WeBWorK Homework: For each section there will be about a dozen homework problems to complete using WeBWorK. These exercises focus on computational skill and basic conceptual understanding and build upon your first contact with Calculus material you gain through Guided Practice.
• WeBWorK Journal: Students will record their work on WeBWorK homework problems following the specification guidelines.
• Daily Quizzes: At the beginning of each class period where we begin lecture on a new section we will have a quiz to assess how well you have mastered the material of the previous day.
• Miniprojects/Problems: The exams will test mastery of the 16 course learning objectives. Each of the exams will consist of problems that where student scan show mastery of the learning outcomes that were part of the chapter. In addition to the Problems, there are eleven miniprojects that involve a careful write-up of your solution. Most Miniprojects focus on real-world applications and the use of real-world data and, especially, the use of technology to model and solve problems involving calculus. Three of the miniprojects ask students to take on the role of teacher by creating lessons that show that they have mastered the material and are able to communicate it in a thorough and efficient way to an audience of their classmates. These teaching Miniprojects are of three types.
  • Texting Lesson Students can create a mock question-and-answer session where a teacher teaches the students one of the core lessons of the class.
  • Video Lesson The student will create a screencast video (or some other type of lesson video) summarizing one of the sections of the book.
  • Desmos Activity Students will create a Desmos account at https://teacher.desmos.com and create a lesson activity that illustrates one of the core objectives of the class.

Grading System Math 181 uses a points-free mastery-based grading system that is designed to provide you with control over the grading process, transparency as to your progress toward a course grade, and a final course grade that truly reflects your actual mastery of course concepts. Our grading system works as follows:

• At the beginning of the semester, you will be asked to decide on the target grade you plan to earn for the course. This does not need to be an “A”. You’ll be asked to carefully consider your goals, skill set, life situation, academic needs, and so on before stating your target grade. For some students, a “B” or even a “C” is perfectly sufficient and realistic, relative to their situation.
• The means of assessing your graded work in the class is done without using points. Instead, your work is graded on a two-level scale of Pass/No Pass. Whenever you submit work to be graded, I will employ my best professional judgment along with a clear list of specifications for categorizing that work. The specifications for your work are provided in a separate page, and you should make yourself intimately familiar with that document. Each Guided Practice, WeBWorK Homework, WeBWorK Journal, and Daily Quiz, Problem, and Miniproject will be graded on a Pass/No Pass basis.
• The grade you earn at the end of the semester is determined by counting the number of items in each category that you PASS. There are no points involved and no statistical or numerical calculations.

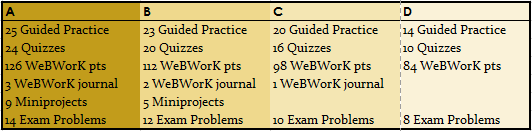
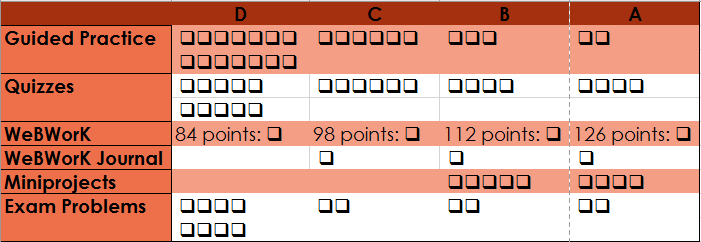
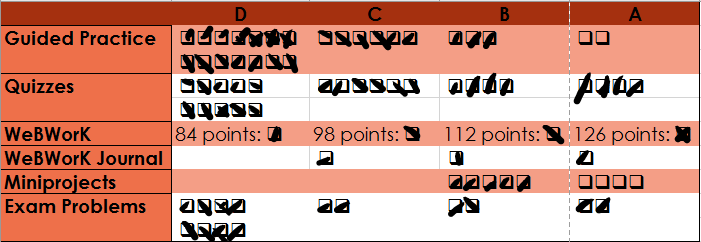
The table for determining your grade is given below. For reference: there are a total of 27 problems and miniprojects, 27 daily quizzes, 28 guided practice assignments, and 140 points of online homework. See the Specifications for Student Work page to see what it means to obtain a PASS.

It might be easier to visualize the grading system as a collection of checkmarks

Plus/Minus grading: In case not all of your attainments in the class are at the same grade level, we will figure plus/minus grades as follows. Note there are five overall categories of work you will do: Guided Practice, Daily Quizzes, Problems/Miniprojects, WeBWorK HW, and WeBWorK HW Journals. First, find your category at which you have attained the lowest level of work. If that is the only category at this level, you will receive a “minus” grade for the next level up. If there are two categories at the lowest level you will receive a “plus” grade. Otherwise (more than two categories at that lowest level) you will receive the grade of your lowest level.

• Example: A student who has passed 23 Guided Practice assignments (B level), 17 Daily Quizzes (C level), scored 140 points on WeBWorK (A level), passed 3 WeBWorK Journals (A level), passed 5 Miniprojects (B level), and passed 12 exam problems (B level) receives a B- since the lowest grade was a C while all the others were at a higher level.

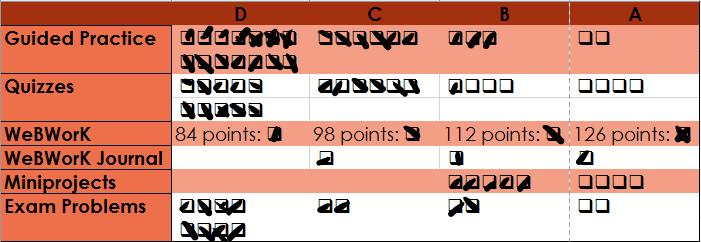
• Example: A student who has passed 23 Guided Practice assignments (B level), 25 Daily Quizzes (A level), scored 132 points on WeBWorK (A level), passed 3 WeBWorK Journals (A level),passed 5 Miniprojects (B level), and passed 15 exam problems (A level) receives a B+ since the lowest grade was a B, but there were only two grades at that level.

Please note that NSC does not award grades of A+ or D-.

Revisions: Instead of partial credit, you will receive numerous opportunities to revise and resubmit work that does not meet the specifications for Passing. Specifically:

• Online homework gives instant feedback on correctness when you submit it. You are allowed unlimited reattempts on every online homework item until the due date.
• Each Daily Quiz can be attempted twice without penalty (an initial attempt + one reattempt in my office). Further reattempts can be “purchased” using tokens (see below).
• Problems are assessed on Midterm and Final exams. If you fail to PASS a learning outcome on the exam, then you can attempt that problem type on the last day of class in the Bonus Final. Once you PASS enough problems for the grade you want, you can opt out of the exams. It’s not uncommon for many students not to take the Final exam or Bonus Final because they have already “leveled up” to their target grade by the time of the exam.
• Any miniproject submission that does not attain a PASS level can be revised and resubmitted for regrading at the expense of a token. * Note: Guided Practice assignments may not be revised or submitted late. These must be completed at the stated deadline or they receive a permanent No Pass.

Tokens: Each student will be given 5 “tokens” at the beginning of the term. Each token can be cashed in for one of the following:

• A revision of a Miniproject that was assessed as a No PASS (within one week of receiving the grade).
• A revision of a WeBWorK journal (within one week of receiving the grade)
• A third attempt of a Quiz (within a week of taking the first quiz).
• A 24-hour extension on any Miniproject or WeBWorK set. If you choose to use a token for a deadline extension, you must inform me prior to the original deadline. Submissions given after the extended deadline are not accepted.

Opportunities to earn additional tokens may be given during the semester.

Notes about this grading system: The advantages of this grading system are numerous:

• It focuses course work away from point-scoring, which is counterproductive to learning, and focuses instead on whether or not your work meets professional quality standards.
• It places control of your grade firmly in your hands so that you don’t have to “hope” for a grade.
• It directly links the grade you earn to the amount and quality of work that you do.
• It gives a final grade that communicates real information about your mastery of the subject.
• Finally, it allows you to be graded on what you eventually master, so that early missteps do not have to have a major negative future impact.

The chief downside to this system is that it’s complicated. You can download my sample gradebook to track your progress through the course to help make it easier. And if you have any questions or concerns about the system, please let me know.

What are the consequences of missing class?

If you miss class you will miss out on the daily quiz. The quiz will only be given to students in class; you will need to use one of your tokens if you want to take a quiz outside of class. If you miss class, then you will also miss out on the lecture and activities. One possible way to catch up on the material that was covered during class is to watch the lecture recording which can be accessed by clicking on the YuJa tab in Canvas. However, you should only think of the recorded lecture as a backup because there are occasionally technical problems.

Note that the style of this class is a partially flipped class, so you will do much of your learning by reading and watching videos outside of class. Much of each class period will be devoted to applying the principles and practicing the techniques that will be acquired in the out-of-class reading. You probably don’t want to miss out on the classroom discussion and activities. If you must miss class, then be sure to complete the Guided Practice prior to class.